Muestreo e inferencia estadística

Distribución Normal

Una de las distribuciones más importantes que podemos encontrar es la distribución normal, gran número de procesos naturales siguen esta distribución. Esta distribución depende de dos parámetros la media () y la desviación típica ().

Diremos que una variable aleatoria X sigue una distribución normal y lo notaremos como si puede tomar cualquier valor real y su función de distribución es:

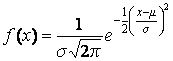
Características de la función de distribución:

• Es simétrica respecto a la media
• El área limitada por la curva y el eje de abscisas (eje x) es 1. Quedando la mitad de ese área a la izquierda de la media y la otra mitad ala derecha
• Toma el máximo valor en la media.
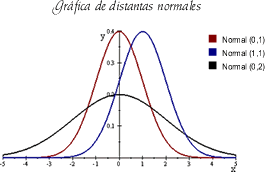
• Si tenemos dos distribuciones con igual media y distinta desviación típica estará más abierta aquella cuya desviación típica sea mayor. Fíjate en la gráfica y compara N(0,1) y N(0,2).

Tipificación de una normal.

Tipificar una distribución normal consiste en realizar un cambio de origen y escala en la distribución original para obtener una nueva distribución que será N(0,1).
Consideremos una variable aleatoria entonces la variable aleatoria sigue una distribución N(0,1) .
El hecho de poder tipificar las distribuciones normales nos permite calcular la probabilidad en cualquier distribución normal conociendo los valores que toma la N(0,1)