Muestreo e inferencia estadística

Intervalo característico

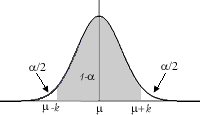Sea X una v.a. que se distribuye normalmente, un intervalo característico es un intervalo simétrico entorno a la media ( -k, +k) en el que la probabilidad de que un valor de la variable esté en ese intervalo es p, es decir :
P[ -k < x < +k] = p.
Llamamos valor crítco a la probabilidad que dejamos fuera del intervalo característico y lo notaremos con . Es claro entonces que la probabilidad que queda en el intervalo será p = 1-.

Intervalo característico en la N(0,1)

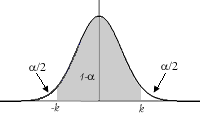Si tenemos la distribución Z->N(0,1) la media es 0, por tanto los intervalos caractarísticos son de la forma (-k, k).
Vamos a calcular los intervalos característicos para los valores más comunes que toma .

Buscamos k tal que P[-k< x <k]=1-
P[-k< x <k]=P[x<k] - P[x<-k]=P[x<k] -1+ P[x<k]=
2·P[x<k]-1, entonces 2·P[x<k]-1 = 1-
P[x<k] = 1 - /2
Nota: Si llamamos al valor de la variable que deja a su derecha una probabilidad , es decir, P[x > ] = . Entonces se tiene que P[x < ] = 1 - /2

Si =0.1 entonces 1-=0.9 y /2=0.05
Hay que hallar k tal que P[ x <k] = 0.95
Buscamos en las tablas y k= 1.645
En N(0,1) el intervalo característico cuyo valor crítico es 0.1 es: (-1.645 , 1.645)

Si =0.05 entonces 1-=0.95 y /2=0.025
Hay que hallar k tal que P[ x <k] = 0.975
Buscamos en las tablas y k= 1.96
En N(0,1) el intervalo característico cuyo valor crítico es 0.05 es: (-1.96 , 1.96)

Si =0.01 entonces 1-=0.99 y /2=0.005
Hay que hallar k tal que P[ x <k] = 0.995
Buscamos en las tablas y k= 2.575
En N(0,1) el intervalo característico cuyo valor crítico es 0.01 es: (-2.575 , 2.575)