Variable Aleatoria
Se define la varianza como la esperanza del cuadrado de la diferencia entre la variable y su esperanza:
V(X) = E[ (X - E[X] )2 ], teniendo en cuenta la definición de esperanza, la varianza queda
Desarrollando el cuadrado llegamos a una expresión de la varianza más cómoda para operar que la definición
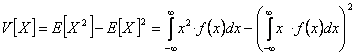
Desviación típica
Se llama desviación típica o estándar a la raíz cuadrada positiva de la varianza 
Para determinar la varianza hemos elevado los datos al cuadrado, esto implica que las unidades se elevan al cuadrado. La desviación típica consigue tener las desviaciones en la misma unidad que los datos.
Ejemplos:
1. El peso (en gramos) de un insecto se distribuye según 
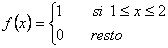
Determínese la varianza de X
Para determinar la varianza primero calculamos E[X] y E[X 2]
-
-
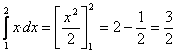
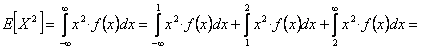
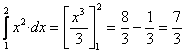
V(X)= E[X 2] - E[X] 2=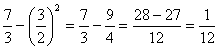
Determínese la varianza de X
Para determinar la varianza primero calculamos E[X] y E[X 2]
-
-
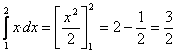
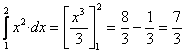
V(X)= E[X 2] - E[X] 2=
2. El tiempo de vida (en años) de una determinada componente de un juguete electrónico tiene por función de densidad
Halla su varianza
Razonamos de forma análoga al caso anterior
- 
- 
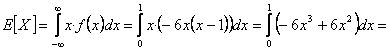
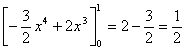
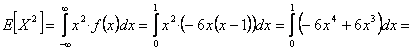
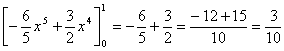
V(X)= E[X 2] - E[X] 2=