Tablas estadísticas

Cuantitativas continuas

Tabla para variable cuantitativa continua

Una variable cuantitativa continua puede tomar todos los valores reales comprendidos entre un valor inicial y un final. Estos valores los vamos a agrupar en intervalos de la forma
( l _i , l _i+1 ]. Diremos que x pertenece al intervalo ( l _i , l _i+1 ] si , como se puede observar el intervalo que hemos tomado es semicerrado por la derecha, normalmente los intervalos suelen ser semicerrados para tomar todos los valores posibles y evitar que un mismo valor pueda entrar en dos intervalos distintos.
Llamaremos amplitud de un intervalo ( a_i ) a la distancia existente entre sus extremos, es decir, a_i = l _i+1 - l _i. Para el cálculo de medidas de centralización y dispersión será necesario usar un representante de cada intervalo, a ese representante lo llamaremos marca de clase y será el punto medio del intervalo, esto es, .

La tabla de frecuencias para una variable cuantitativa continua tiene la siguiente estructura:

Modalidad	Marca de clase	F. Absoluta	F. Relativa	Porcentaje	F. Abs. Acumu.	F. Rel. Acumu.
(li, li+1]	xi	ni		pi=100 fi

Elección de intervalos para variables continuas
A la hora de seleccionar los intervalos para las variables continuas, se plantean varios problemas como son el número de intervalos a elegir y sus tamaños.

El número de intervalos, k, a utilizar no está determinado de forma fija y por tanto tomaremos un k que nos permita trabajar cómodamente y ver bien la estructura de los datos; Como referencia nosotros tomaremos una de los siguientes valores aproximados:

1. Si n es pequeño tomaremos como número de intervalos
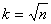
2. Si en cambio n es grande tomaremos

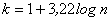
Por ejemplo si el número de observaciones que tenemos es n=100, un buen criterio es agrupar las observaciones en intervalos. Sin embargo si tenemos n=1.000.000, será mas razonable elegir intervalos, que

¿Cómo determinamos los intervalos?

1. Tomemos el conjunto de datos y lo ordenamos de menor a mayor.
2. Consideremos el rango de los datos, es decir, la diferencia entre el valor menor y mayor R = x_mayor - x _menor
3. Determinamos k usando una de las dos fórmulas anteriormente expuesta, en función del número de datos.
4. Vamos a considerar intervalos con igual amplitud, y ésta será 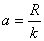. Puede que el valor que hemos determinado sea un número poco estético y sea más útil redondearlos, por ejemplo supongamos que a = 15.12654 tomaríamos a = 15, análogamente podemos hacer lo mismo con x _menor o x_mayor.

• Determinamos los extremos de los intervalos
  • l ₀ = x _menor o l ₀ = x _menor(redondeado).
  • l ₁ = l ₀ + a
  • En general l _i = l _i-1 + a